my colour short course is
now offered online through
Australia's National Art
School in Sydney! There's
a choice of two sessions to
suit every time zone. LINK
Home
The Dimensions of Colour
Basics of Light and Shade
Basics of Colour Vision
Additive Mixing
Subtractive Mixing
Mixing of Paints
Hue
Lightness and Chroma
Brightness and Saturation
- Brightness, Saturation and Colourfulness
- RGB, CMY and CMYK Colour Space
- HSB (=HSV) Colour Space
- HLS (=HSL) and HSI Colour Space
Afterthoughts
Glossary
References
Contact
Links
NEXT COLOUR
WORKSHOPS

BRIGHTNESS-BASED COLOUR SPACES 1: RGB, CMY AND CMYK SPACES
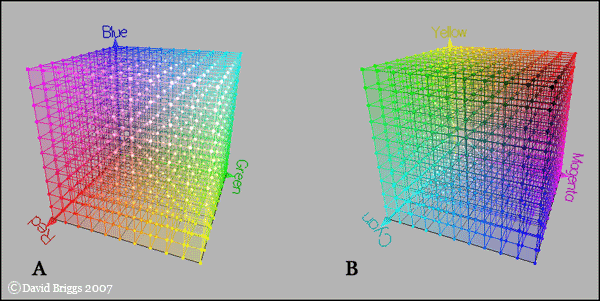
Figure 9.2. RGB and CMY colour space. (A) RGB and (B) CMY colour spaces, illustrated using the programme RGBCube by Philippe Colantoni.
RGB SPACE
Since the colours on a computer monitor or television are produced from various combinations of R, G and B components, it follows that they can be represented by a system of three orthogonal axes representing these components. This results in a cubic volume enclosing all possible screen colours, with black at the origin and white at the opposite corner. Easygoing artists like ourselves can refer to this as RGB colour space, but when mixing in strict colourimetric circles, take care to refer to it as the RGB colour model, which can be embodied in various defined colour spaces, such as sRGB or AdobeRGB.
The R,G and B components are usually reported on a scale of 0 to 255, but can also be reported on a scale of 0 to 1 (distinguished as r,g and b here). Confusingly, these RGB values sometimes refer to linear units of light energy, or radiance, and sometimes to nonlinear units of perceived brightness (i.e. in equal perceptual steps). Often no care is taken to show which of the two kind of units is being used - you need to work it out in each context (link). In Photoshop, both relative brightness (B) and the R,G and B components are reported in nonlinear (brightness) units.The conversion is:
(nonlinear) brightness = linear "brightness" 0.45
The formula has a generally similar effect to the more elaborate nonlinear conversion between CIE luminance (Y) and Lightness (L),
L = 116 (Y/Yn)1/3 - 16; 0.008856 < Y/Yn
CMY SPACE
In CMY space, the same RGB colours are considered as subtractive mixtures of
varying quantities of cyan (C), magenta (M) and yellow (Y) colourants. The resulting
cubic space is identical to RGB space, apart from the fact that the origin of
the C, M and Y axes is at the point representing white instead of black (Figure
9.2B). The conversion is given by the formulae C = 255 minus R (or 1 - r), M
= 255 minus G (or 1 - g), and Y = 255 - B (or 1 minus b) respectively (Figure
9.3). Note that C, M and Y in these formulae refer to the ideal subtractive
primaries, not actual cyan, magenta and yellow inks, i.e. C,M and Y behave as
ideal subtractive colourants complementary to the particular R,G and B additive
primaries that are in use.
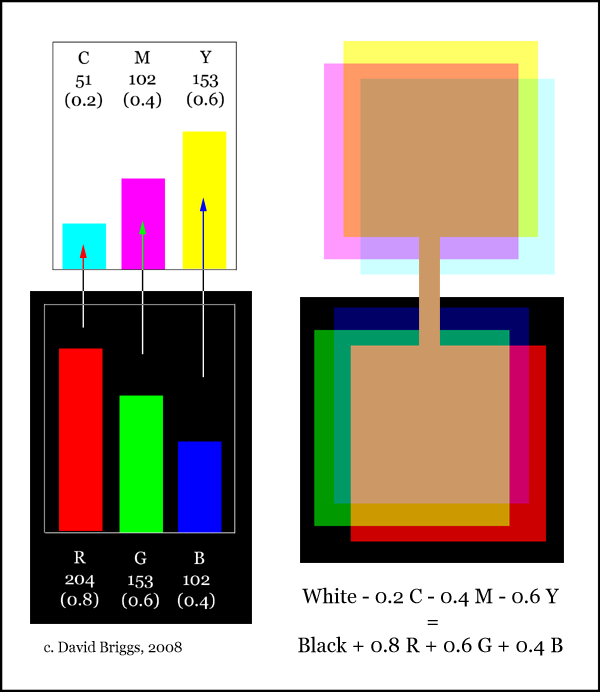
Figure 9.3. Ideal conversion of RGB to CMY.
CMYK SPACE
Although cyan, magenta and yellow inks might be expected be sufficient for colour printing, most actual colour printing uses black ink in addition. This is partly because a mixture of the first three inks may not yield a black that is neutral enough, or dark enough, but also because the use of black spares the use of the more expensive coloured inks, and also reduces the total amount of ink used, thus speeding drying times. Conversely, it permits the use of coloured inks with better colour rendering properties than would be possible if it was necessary that these mix to make a dense black by themselves. The practical need for a black component was recognized right from the invention of colour printing by the German artist J.C. Le Blon in the early 1700's. After Le Blon's death his former pupil, Jacques Gautier D'Agoty, in order to protect his own patent for the four-colour process, disputed the claims of Le Blon's workshop that the master had ever used more than three colours. Le Blon 's supporters replied that their master kept quiet about his use of the fourth plate because he used it in spite of himself, and felt that it would dishonour his system (Gage, 1999, p. 139).
The amount of the black component needed is conventionally specified by the letter K. CMYK values are typically reported as percentages. Ideal CMYK values can be calculated by simple formulae directly from CMY values, but these values are not accurate for colour printing (Ford and Roberts, 1998):
Black (K) = minimum of C,M,Y
CyanCMYK = (C - K)/(1 - K)
MagentaCMYK = (M - K)/(1 - K)
YellowCMYK = (Y - K)/(1 - K)
These "cheap and nasty" formulae for CMYK in effect divide the CMY values into a black component (determined by the minumum value among C, M and Y), and the relative proportions of C, M and Y within the remaining coloured component (Figure 9.4). In ideal CMYK, one of the C, M or Y values is therefore always zero.
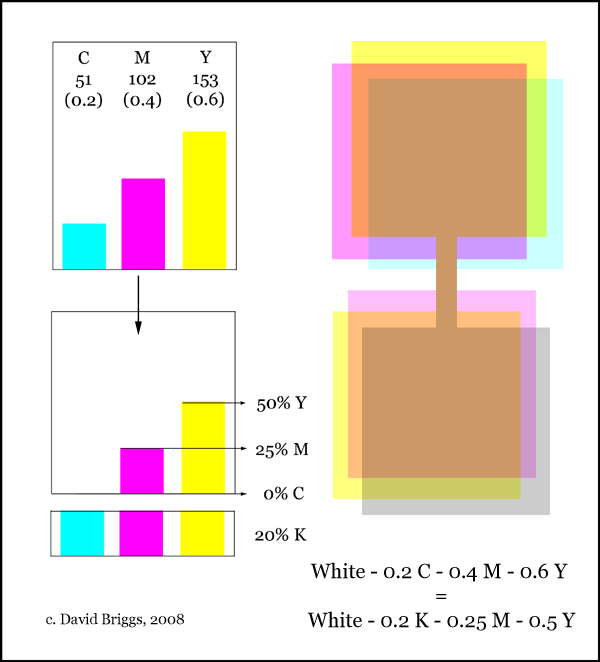
Figure 9.4. Ideal conversion of CMY to CMYK. Though this idealized conversion is only indicative, it at least suggests how the use of black ink can permit the same result to be obtained using less coloured ink, and less ink overall, than with three coloured inks alone.
The conversion to CMYK values given by the colour picker in Photoshop does not use these simple formulae, but is a much more sophisticated colour management transformation (via Lab space) that takes account of the colour profiles of the monitor display and printer inks specified by the user.
