PART 5. SUBTRACTIVE COLOUR MIXING

DEFINITION

If we shine light separately through two coloured filters and combine the beams, the colour mixing process is, as we have just seen, an example of additive mixing. A different kind of colour mixing occurs if we place the same filters on top of each other, and shine light through the combined filters. This kind of colour mixing is generally called subtractive, because each filter in turn removes light from the original amount. The colour stimulus that results depends on what wavelengths are transmitted by both filters. Subtractive mixing is of great importance to painters using traditional paint mediums because the processes of physical mixing of paints and glazing are both largely subtractive in their effects (though not entirely, as we all see in the next section).

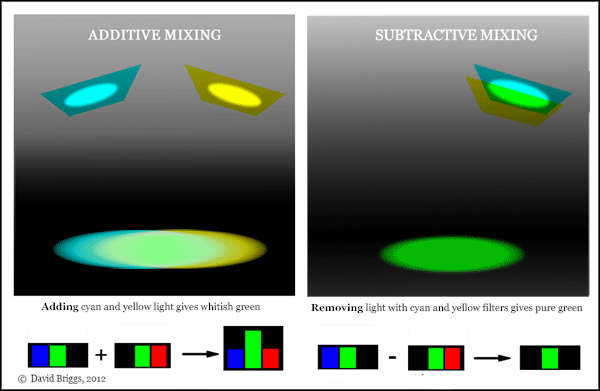
Figure 5.1. Effects of additive and subtractive mixing contrasted using yellow and cyan filters. Adding cyan and yellow light gives greenish white light; removing light with cyan and yellow filters gives saturated green light.

The colour stimulus resulting from the interaction of a coloured light source and a coloured object is also a type of subtractive mixing, if we think of the incident light as having had certain wavelengths removed compared to white light.

Figure 5.2. Cyan coloured ball under yellow light. IMAGE: D. Briggs, Photoshop CS2.

HOW SUBTRACTIVE MIXING WORKS

In detail, the result of this subtractive mixing can be calculated from the product of the percentage transmission of light by both colourants, for each wavelength of the visible spectrum. (This has led some writers to prefer the term multiplicative mixing). In Figure 5.1, our yellow filter transmits a high proportion of light in the red-orange and green bands of the spectrum, while our cyan filter transmits light in the green and blue-violet bands. Subtractive mixing produces the colour these filters have in common: in this case, green.

Note well that a yellow colourant does not, as is sometimes stated or assumed, reflect or transmit wavelengths mainly in the yellow part of the spectrum, and absorb all other wavelengths. (Authors of several well-known books and websites on colour have revealed their ignorance of the first principles of their subject by this error). High-chroma yellow colourants characteristically pass on most light in the red, orange, yellow, and green bands of the spectrum, and absorb most light in the blue and violet bands.

Take a moment at this point to also ensure that you have completely eradicated from your mind every trace of the primary school notion that green is "made of" yellow and blue. Subtractive mixing doesn't work like that. We get a green mixture from yellow and cyan because our components are both in part "made of" green. If any colour can be said to be "made of" yellow and blue, it's white.

We saw earlier that two colourants may look identical in appearance, but have fairly different spectral absorption curves. Because of this phenomenon, known as metamerism, the exact results of subtractive interaction of real colourants can not be predicted from their colour. This uncertainty should not be overstated, however: any actual cyan and yellow filters combined subtractively will make a green, though the precise appearance and spectral composition of that green will depend on the spectral absorption curves of the components.

Subtractive mixing in digital mediums, unlike traditional mediums, is entirely simple and predictable, in that our virtual colourants act as ideal filters, and there are only three bands of the spectrum to be considered. In Photoshop, ideal subtractive mixing is seen for example when colours mix in multiply mode. In programs such as Painter that cleverly simulate the appearance and physical behaviour of artists' paints, colours nevertheless still mix by ideal subtractive mixing (e.g. yellow and deep blue mix to make black or grey, not green).

<< 1 2 3 >>